In a previous post we explored patient clustering. The somewhat discouraging conclusion I arrived at was that patient clustering might not be as informative as I hoped, with many of the clusters I identified being non-specific to the cohort I was clustering (e.g. any cohort, including the general population, has a distinct cluster of pregnancy / giving birth).
Just thinking out loud, but it seems the real question I’m often interested in isn’t ‘is this cohort heterogeneous?’, but instead ‘is the way in which this cohort differs from the general population heterogeneous?’. I know this immediately begs the question what the general population is, but let’s put that issue aside for now. To go back to the example of diabetes, I would expect type 1 and type 2 to differ from the general population in different ways. Pregnant women can have type 1 or type 2 diabetes, so pregnancy is not a distinguishing feature, but other features can be distinguishing in this sense.
One way to formalize this idea is to frame it as a prediction problem. As we know, in OHDSI a prediction problem requires identifying a target cohort (T) and an outcome (O). For example, T can be patients visiting the doctor, and O can be diabetes. We can then for example aim to predict which people in T develop O in the year after the visit. Normally we’d fit something like a (regularized) logistic regression using a formula like:
![]()
Where P(O=1) is the probability that a person has the outcome, f(.) is the logistic link function, beta is a vector of coefficients to optimize, and X is a vector of features.
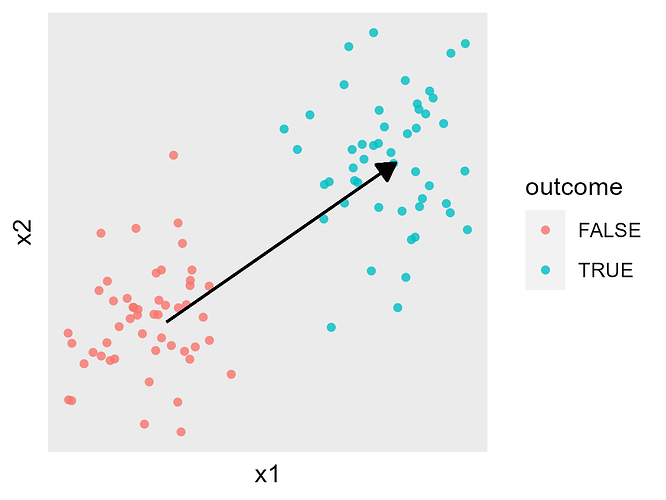
The figure below shows this in a simple cartoon, where X has two continuous components (x1 and x2), and the arrow represents the beta we’re trying to fit:
What is instead we formulate this as a mixture? So the problem can be formulated as:
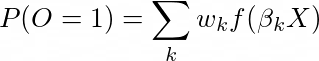
Where the mixture has k components, each with a vector beta_k and a weight w_k, where the sum of w_k equals 1:
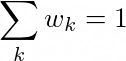
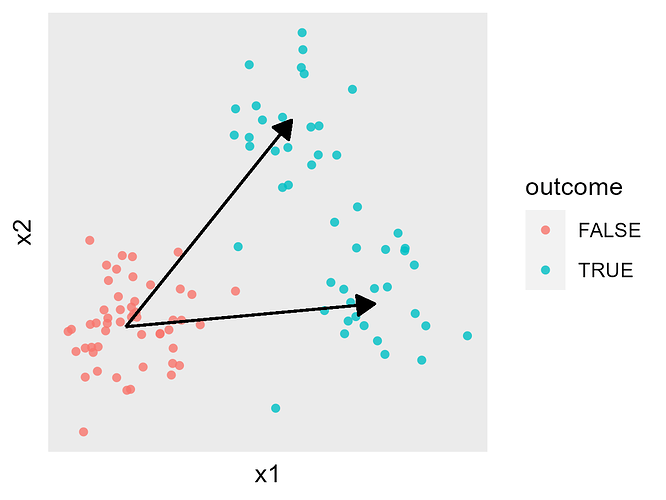
Again as a simple cartoon, each beta_k vector would correspond to one of the arrows:
Each vector beta_k would describe one of the ‘clusters’ I’m interested in. All I need to do is fit the model with a range of values for k, find the best fit, and I’m done ![]()
One the one hand this seems like an obvious thing to do, so has it already been done before? Does anybody know of solutions that have already been used, maybe in other domains?
On the other hand I’m guessing this is an ill-defined problem. Multiple combinations of w and beta can produce the same likelihood. This is also not a convex likelihood function. Can we reformulate it as such?