dear @schuemie , @Patrick_Ryan , and all,
i have been reading thoroughly the paper empirical CI calibration by martijn et al, and i have a concern that i hope you can address: it looks to me as if the assumption beyond the construction of positive controls is equivalent to assuming that the outcome variable is measured without error.
this is the statement that puzzles me.
“We exploit the negative controls to construct synthetic positive controls by injecting simulated outcomes during exposure. For example, assume that, during exposure to dabigatran, n occurrences of ingrowing nail were observed. If we now add an additional n simulated occurrences during exposure, we have doubled the risk. Since this was a negative control, the relative risk compared with warfarin was one, but after injection, it becomes two.”
to my understanding, the idea here is that since n cases are observed in exposed, and the risk in exposed and non exposed should be the same (because it’s a negative control), then injecting n simulated occurrences during exposure should produce a new ‘true’ variable (half original and half simulated) which has a double risk among exposed wrt to the negative control, and therefore a ‘true’ RR=2.
let me start from a simple example of a negative control where this seems not to be working: presbyopia. in this case, almost all of the study population (warfarin or dabigatran users) is older than 45 and we can safely assume that they almost all have presbyopia, regardless of exposure. however, it is well possible that only n people exposed to dabigatran have a record of presbyopia (n smaller than the people exposed), since it is a condition that in itself requires mild or no medical attention - for instance you can safely bet that this is what happens in my own database. as a consequence, when we add additional n simulated occurrences during exposure to dabigatran, we pick no new ‘true’ cases! so the ‘true’ risk of the positive control among the exposed remains the same as the risk of the negative control, therefore the ‘true’ RR of the positive control is still 1.
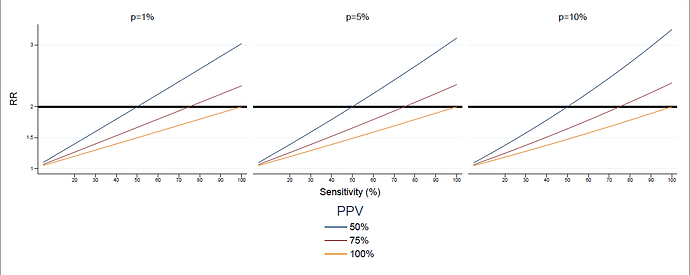
let’s now go to a less extreme negative control: obesity. event though, in this case, not all the exposed to dabigatran are obese, obesity is a highly prevalent condition among adults - safely more than 10%. at the same time, the outcome may well have imperfect sensitivity: for instance, i am confident that the vast majority of obese people cannot retrieved as such from my own database. so obesity is a case with high prevalence and (perhaps, only in some databases) low sensitivity. some computations then show that even in this case, when injecting n occurrences among the exposed, the RR increases by less than a factor 2. the reasons are two. first, when we select randomly the new cases, we must expect to pick some obese that we had not noticed, so we are in fact adding less than n cases; second, the true risk of obesity among exposed (that balances against the risk among unexposed) is not the observed risk, but the true risk. so, if we add a number of occurrences similar to the number of observed obese, we increase the risk proportional to the observed risk of obesity, not proportional to the true risk of obesity: as a consequence, we increase the risk by a factor which is discounted by the proportion of obese that we don’t observe.
let me do the math. the n cases of obesity observed in the exposed are a small percentage of the true cases of obesity: say that there is a number k bigger than 1 such that the true number of exposed obese is kn. therefore among the exposed there are (k-1)n true obese people that did contribute to the true risk, but that could not be observed from the data. now we inject n additional simulated occurrences, picked randomly among the N-n that we observed as non obese, N being the total number of persons in the exposed study population. the two problems mentioned above can be quantified as follows, where we denote by p the prevalence of obesity, that is, p=nk/N
problem 1) we must expect to pick randomly some of the (k-1)n true obese that we had not noticed. on average, the proportion of true obese among the n injected is (k-1)n/(N-n), or (after some computations) (p-p/k)/(1-p/k). therefore the number of new cases among exposed in the positive controls is not n but n(1-(p-p/k)/(1-p/k))=n(1-p)/(1-p/k). in short:
true new cases= n(1-p)/(1-p/k)
if p is 10% and k is 4 (so, a sensitivity of 25%), this factor is .92.
problem 2) the true cases of obesity in the exposed are kn, so the relative risk in the exposed of the positive control wrt the negative control is
(kn+(true new cases))/kn=(kn+n(1-p)/(1-p/k))/kn=1+(1/k)(1-p)/(1-p/k)
if p is 10% and k is 4, this is 1.23: the risk of the positive control in the exposed is therefore much smaller than 2.
and finally, notice that in the previous computations we have made no use of the fact that the prevalence of obesity is high. if prevalence is low, the first problem is in fact not relevant, but unfortunately the second problem is only dependent on sensitivity: if p is close to 0, the formula is approximately 1+1/k. in summary: when sensitivity is low, the positive control built by doubling the observed cases has a smaller RR than 2.
and a similar problem, in the opposite direction, could be argued if PPV is low: then the positive control has a higher risk than 2.
so, if i am right, the assumption in the sentence at the beginning of this message is equivalent to PPV=sensitivity=100%.
but, as i said, i would be happy to be proven wrong!
looking forward to the authors’ and others’ feedback!
rosa
) have low prevalence, though, because what we are interested in here is the prevalence among exposed, not in the general population. in the specific case, there are several negative controls which are related to diabetes, which is highly prevalent among dabigatran users, and p is likely to be much higher here than in the general population. so this is something that could be usefully included in the pipeline for generating the positive outcome: indeed if scenarios on sensitivity are tested, then p can be estimated by kn/N.