Hi all. I wanted to help structure the discussion on this topic a bit, and add my 2 cents:
Note: I’m here deliberately avoiding the term “phenotype”, because recently people have stressed that a phenotype is a set of people with certain characteristics. An outcome on the other hand is an event that occurs in peoples’ lives, and most importantly has a date of onset, whereas a phenotype does not.
Because the data we have often was not collected for the purpose of research, many things we need to know for our analyses are actually not explicitly recorded. This is most pressing when it comes to what we call ‘outcomes’: events that happen in patients’ lives that are either good or bad, may have been caused by something else, and perhaps could have been predicted and/or prevented. To construct outcomes for our analyses, we therefore often rely on complicated logic that uses the data we do have. For example, if we want to find people who have experienced an acute myocardial infarction, we may require diagnosis codes in combination with procedure codes for the diagnostic tests, and maybe even treatment codes. The question remains: what is the right set of logic, and how well does a specific set of logic perform in terms of sensitivity and specificity?
In the past, work in OHDSI has focused on learning the logic from the data, but that had some mayor limitations, such as strong requirements on the data, and not being able to pinpoint the date of onset of the outcome.
So now we’re considering using manually crafted cohort definitions based on expert knowledge, as is the status quo in observational research, and finding better ways of evaluating these. I’ve created a Venn diagram in Figure 1, showing the group of people that truly have the outcome, and the group of people in a cohort (e.g. meeting an ATLAS cohort definition). Based on the insersection (true positives) of the two groups, and the number of people in one group but not the other (false negatives and false positives), we can compute important performance metrics such as sensitivity and specificity.
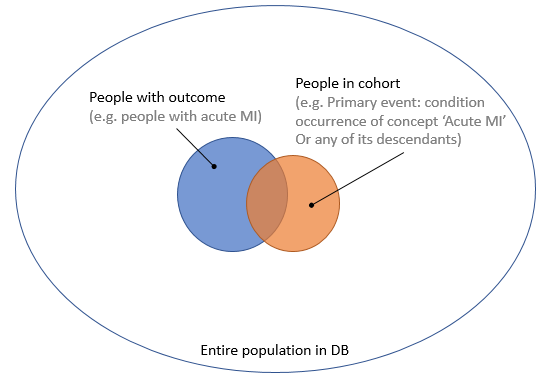
Figure 1. People with the outcome and people in the outcome cohort.
One way to estimate these numbers is to perform chart review: we go back to the original data, read the doctor’s notes, and investigate further to determine with high certainty whether someone really had the outcome. Because this is a lot of work, we typically take a random sample. We could take a sample of the entire population in the database, as this would allow us to compute both sensitivity and specificity. But the outcome is usually rare, and we would therefore need to review a large sample to have some people with the outcome, wasting valuable resources reviewing charts of people who certainly do not have the outcome, as depicted in Figure 2.
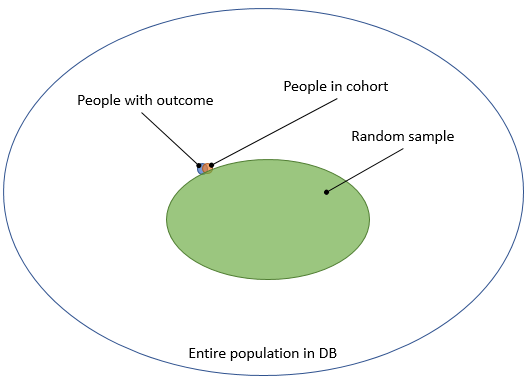
Figure 2. Taking a random sample from the entire population.
To avoid this problem, the typical approach is to take a sample of people that are in our cohort, as depicted in Figure 3.
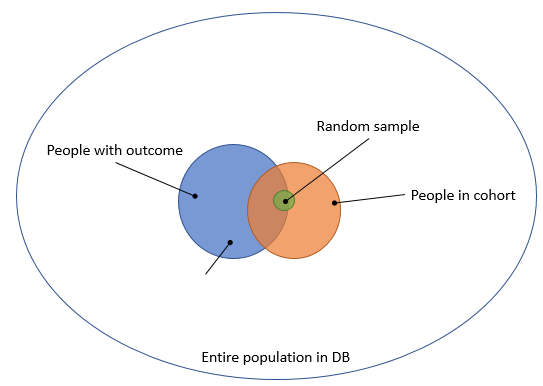
Figure 3. Taking a random sample from the people in the cohort.
The downside of this is that it only allows computation of the positive predictive value (PPV), which is not really what we want to know.
@nigam wrote this proposal to allow computing sensitivity and specificity using a small sample. The basic idea is depicted in Figure 4. (@nigam: please correct me if I’m wrong) Select a group of people that definitely have the outcome (e.g. people that get the treatment for the outcome), and call this set E. Sample 100 people from this group. In addition, sample 100 people that are neither in E nor in the cohort. People in the first 100 are likely to have the outcome, and many will be in the cohort. People in the second 100 are likely not to have the outcome, and are by definition not in the cohort, so all 4 cells of the 2-by-2 table we need will have some data.
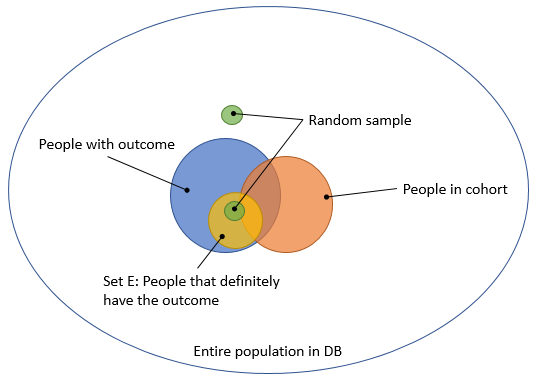
Figure 4. Computing sensitivity and specificity using two small targeted samples.
@jswerdel proposed a different approach: identify a group of people that certainly have the outcome (e.g. people with 5 diagnosis codes), and call this the xSpec (extreme specificity) cohort. Typically, this is a subset of the cohort we’re trying to evaluate. Then, fit a model that predicts whether someone is in xSpec or in the general population. The nice thing about this is that it creates a gradient membership: a lot of people have a predicted probability > 0, but only a few will have a high probability. Joel then proposes identifying the ‘inflection point’ where this probability changes rapidly, and declare everyone with a higher probability than this point to truly have the outcome. This allows us to compute the sensitivity and specificity without performing chart review, and is depicted in Figure 5.
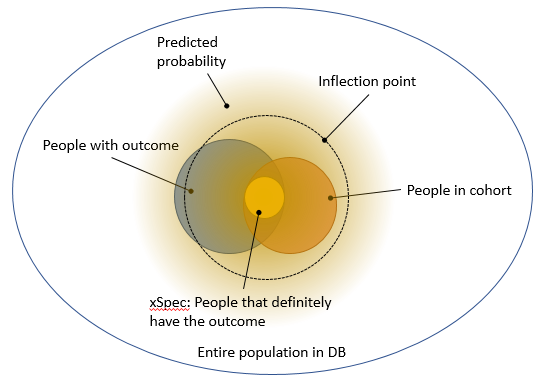
Figure 5. Using a predictive model to separate true from false.
I like Joel’s approach in that it is automatic, and gives an approximate answer without requiring extensive chart review.
My two cents:
My concern with Nigam’s proposal is that it focuses entirely on the extremes, but not on the middle-ground. Probably everyone in the first 100 have the outcome, probably everyone in the second 100 do not have the outcome, so most of the effort is wasted in confirming the obvious.
My first concern with Joel’s proposal, which becomes apparent in Figure 5, is that xSpec might not be at the ‘center’ of the true population with the outcome, and drawing a larger ‘circle’ around it may not fully coincide with the true population. To move from the abstract to a concrete example: imagine xSpec by its definition only includes people that have an MI and then are rushed to the hospital. It may then miss the characteristics of people that have an MI while already in the hospital (just making this up). Another concern is that the inflection point seems pretty arbitrary, although Joel has done some empirical validation there.
One idea that combines Joel’s and Nigam’s: If we want to do chart review, why not focus on the group of people with the highest ‘information’ (in information theory sense)? Sample from the entire population, but give higher sample probability to those people that Joel’s model indicates are ‘on the fence’, so neither certainly without the outcome, or certainly with the outcome. We can later even correct for this weighting to apprimate an unbiased sample.
Anyway, just hoping to keep the discussion moving forward. I think building a validated outcome library has the highest priority, and appreciate everyone working on this!

